01-〽️线性洞察AI本质

💡🧠 深度学习，损失函数，优化器，随机梯度下降等等。这些东西我在做的时候都会这样去做，但我并没有深入的去理解这背后的“数学原因”，仅仅知道一个大概的逻辑原因，为什么能？什么情况下不能？为什么应该？我好像都回答不上来。所以，通过最机器学习里最简单的线性模型，来回顾理解一下AI里本质的数学原因是什么。

0 线性回归模型

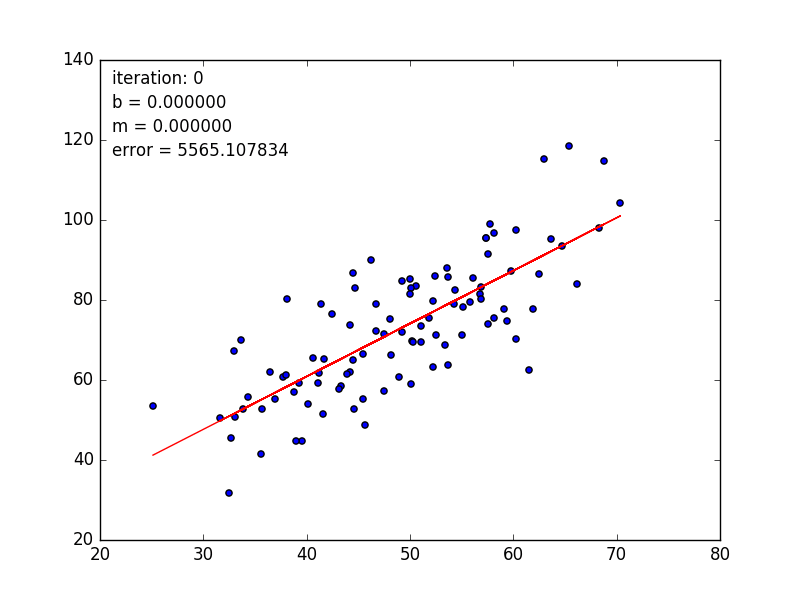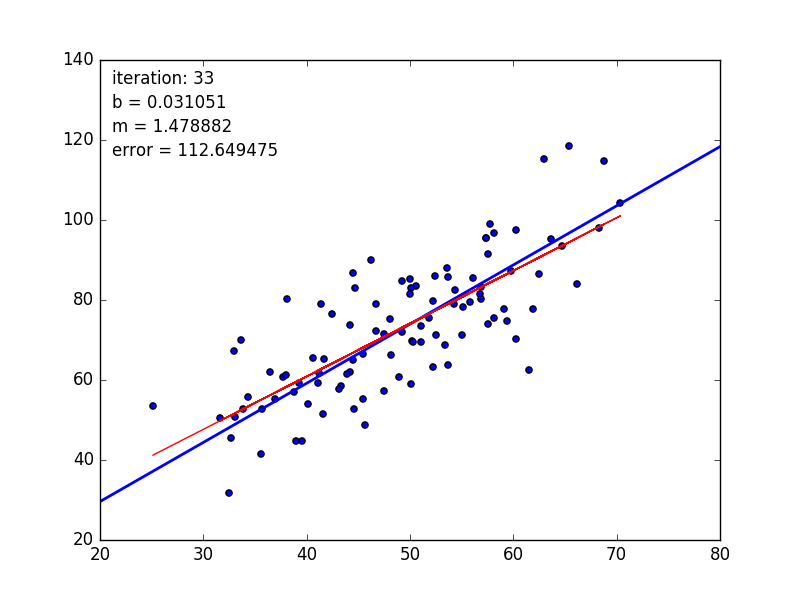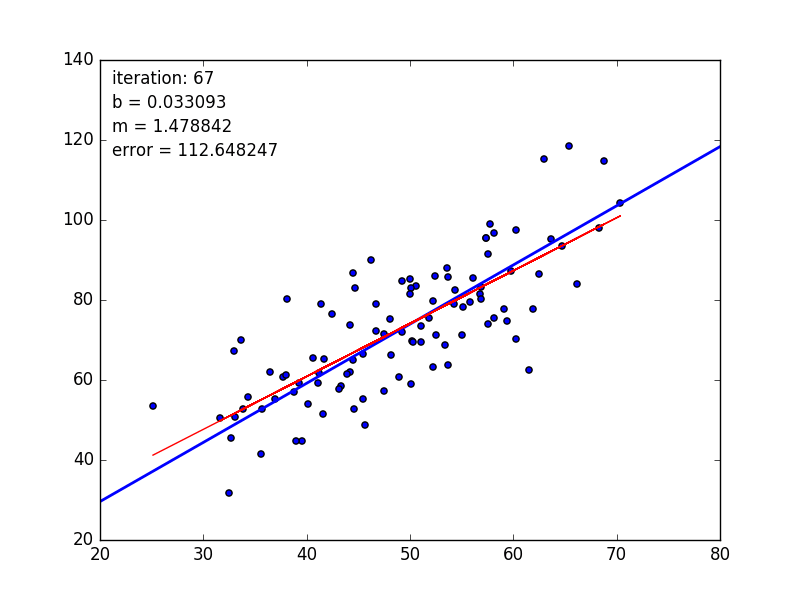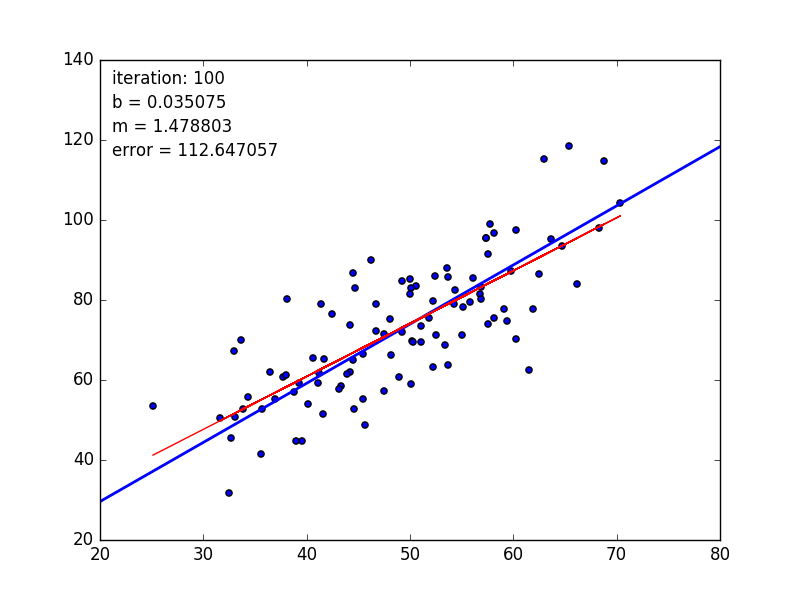
💹 线性回归模型 要做的事情很简单，通过一系列的点去拟合一条总体上最接近所有样本点的直线，近似的表达出这些点的实际分布。

通过数学公式，我们写出线性模型的数学表达式如下：

$$f\left(x_i\right)=\omega x_i+b$$

我们希望最后拟合结果的这个 $f\left(x_i\right)$ 与样本点 $x_i$ 对应的 $y_i$ 其值是尽可能接近的，所以，我们写出如下目标函数：

$$E_{(w,b)}=\sum _{i=1}^m{\left(y_i-w{x}_i-b\right)}^2$$

以上目标函数，其实就是该线性模型与所有样本点之间的均方误差（这里也可以说是最小二乘法估计，最小二乘法是一种优化技术，其目标是将预测值与实际值之间的差平方和最小化），我们需要找到一组参数 $\left(\omega ,b\right)$ ，使得该误差最小，这时我们认为通过这些样本点拟合出来的这条直线，是目前最接近于这些样本点真实分布的一个模型。

确定目标后，我们开始求解。首先观察目标函数 $E_{(w,b)}$ 的具体性质，该函数反应的是误差，我们总可以使模型离样本点无限远，使得该误差无限大，所以该目标函数没有最大值，但一定有一组参数 $\left(\omega ,b\right)$ 使得该误差最小，所以该目标函数存在最小值。找到这个最小值点，高中知识，对目标函数进行求导，使导数为零，该极值点就是最小值点。

$$\begin{array}{rl}\frac{\partial E_{(w,b)}}{\partial w}& =\frac{\partial }{\partial w}\left[\sum _{i=1}^m{\left(y_i-w{x}_i-b\right)}^2\right]\\ & =\sum _{i=1}^m\frac{\partial }{\partial w}\left[{\left(y_i-w{x}_i-b\right)}^2\right]\\ & =\sum _{i=1}^m\left[2\cdot \left(y_i-w{x}_i-b\right)\cdot (-x_i)\right]\\ & =\sum _{i=1}^m\left[2\cdot \left(w{x}_i^2-y_i{x}_i+b{x}_i\right)\right]\\ & =2\cdot \left(w\sum _{i=1}^m{x}_i^2-\sum _{i=1}^m{y}_i{x}_i+b\sum _{i=1}^m{x}_i\right)\\ & =2\left(w\sum _{i=1}^m{x}_i^2-\sum _{i=1}^m\left(y_i-b\right)x_i\right)\end{array}$$ $$\begin{array}{rl}\frac{\partial E_{(w,b)}}{\partial b}& =\frac{\partial }{\partial b}\left[\sum _{i=1}^m{\left(y_i-w{x}_i-b\right)}^2\right]\\ & =\sum _{i=1}^m\frac{\partial }{\partial b}\left[{\left(y_i-w{x}_i-b\right)}^2\right]\\ & =\sum _{i=1}^m\left[2\cdot \left(y_i-w{x}_i-b\right)\cdot (-1)\right]\\ & =\sum _{i=1}^m\left[2\cdot \left(b-y_i+w{x}_i\right)\right]\\ & =2\cdot \left[\sum _{i=1}^{m}b-\sum _{i=1}^m{y}_i+\sum _{i=1}^{m}w{x}_i\right]\\ & =2\left(mb-\sum _{i=1}^m\left(y_i-w{x}_i\right)\right)\end{array}$$

将上式两个导数令其为0，即求解：

$$\begin{array}{r}w\sum _{i=1}^m{x}_i^2=\sum _{i=1}^m\left(y_i-b\right)x_i\\ mb=\sum _{i=1}^m\left(y_i-w{x}_i\right)\end{array}$$

第二个式子可以得出： $b=\frac{1}{m}{\sum }_{i=1}^m(y_i-w{x}_i)$ ，又因为 $\frac{1}{m}{\sum }_{i=1}^m{y}_i=\bar{y}$ ，$\frac{1}{m}{\sum }_{i=1}^m{x}_i=\bar{x}$ ，则 $b=\bar{y}-w\bar{x}$ ，我们将该结果带入第一个式子求解 $w$

$$\begin{array}{rl}w\sum _{i=1}^m{x}_i^2& =\sum _{i=1}^m{y}_i{x}_i-\sum _{i=1}^m(\bar{y}-w\bar{x})x_i\\ w\sum _{i=1}^m{x}_i^2& =\sum _{i=1}^m{y}_i{x}_i-\bar{y}\sum _{i=1}^m{x}_i+w\bar{x}\sum _{i=1}^m{x}_i\\ w(\sum _{i=1}^m{x}_i^2-\bar{x}\sum _{i=1}^m{x}_i)& =\sum _{i=1}^m{y}_i{x}_i-\bar{y}\sum _{i=1}^m{x}_i\\ w& =\frac{{\sum }_{i=1}^m{y}_i{x}_i-\bar{y}{\sum }_{i=1}^m{x}_i}{{\sum }_{i=1}^m{x}_i^2-\bar{x}{\sum }_{i=1}^m{x}_i}\\ w& =\frac{{\sum }_{i=1}^m{y}_i(x_i-\bar{x})}{{\sum }_{i=1}^m{x}_i^2-\frac{1}{m}({\sum }_{i=1}^m{x}_i{)}^2}\end{array}$$

以上求解出 $w$ 后，我们代回 $b=\bar{y}-w\bar{x}$ 就可以求解出 $b$ 了。

• [n] 到此为止，最简单的线性模型，我们就求解完了。回答一下如下几个问题：
• [?] 为什么可以通过求极值点的方式来求解参数？
  • [n] 列出目标函数后，我们需要找到目标函数的最小值。通过分析发现该目标函数没有最大值点，仅存在最小值点，且该函数连续可导，所以其极值点一定就是该函数的最小值点。

1 多元线性回归模型

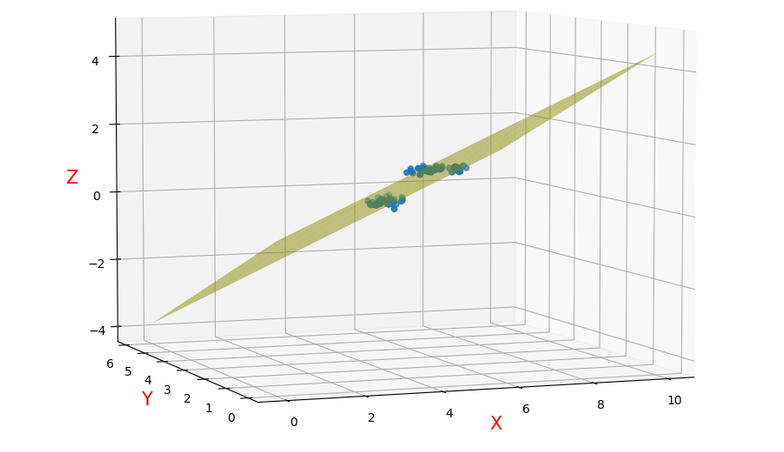
🌈 线性回归模型 中，我们只有一个变量，但大部分现实问题，一个结果往往是由多个因素共同作用所导致的，这就意味着有多个变量，假设我们有 $d$ 个不同属性，我们按照线性回归模型同样的思路进行建模：

$$\begin{array}{r}{w}^T=\left[w_1{w}_2{w}_3\dots w_d\right]\\ x^T=\left[x_1{x}_2{x}_3\dots x_d\right]\\ f\left(x\right)=w^{T}x+b\end{array}$$

以上就是 多元线性回归模型 的数学表达，根据上述思路，我们同样使用 最小二乘法 来对参数 $w^T$ 和 $b$ 进行估计，为了方便表达，我们将两个参数写成一个向量： $\hat{w}=\left(w;b\right)$ ，假设总计有 $m$ 个样本，每个样本 $d$ 个属性，将所有数据融合进一个矩阵中：

$$X=\left[\begin{array}{ccccc}{x}_{11}& x_{12}& \cdots & x_{1d}& 1\\ x_{21}& x_{22}& \cdots & x_{2d}& 1\\ ⋮& ⋮& \ddots & ⋮& ⋮\\ x_{m1}& x_{m2}& \cdots & x_{md}& 1\end{array}\right]$$

再将 $y$ 写成向量形式有： $y=\left(y_1;y_1;\dots ;y_m\right)$ ，最小二乘法 中的平方换到矩阵中就是矩阵的转置与本身相乘，所以，我们写出目标函数：

$$E_{\hat{\mathbf{w}}}=(\mathbf{y}-\mathbf{X}\hat{\mathbf{w}}{)}^{\mathrm{T}}(\mathbf{y}-\mathbf{X}\hat{\mathbf{w}})$$

我们需要目标函数取得最小值，所以对目标函数求导寻找极值点，将目标函数展开如下：

$$E_{\hat{\mathbf{w}}}={\mathbf{y}}^{\mathrm{T}}\mathbf{y}-{\mathbf{y}}^{\mathrm{T}}\mathbf{X}\hat{\mathbf{w}}-{\hat{\mathbf{w}}}^{\mathrm{T}}{\mathbf{X}}^{\mathrm{T}}\mathbf{y}+{\hat{\mathbf{w}}}^{\mathrm{T}}{\mathbf{X}}^{\mathrm{T}}\mathbf{X}\hat{\mathbf{w}}$$

然后对 $\hat{w}$ 进行求导：

$$\frac{\partial E_{\hat{\mathbf{w}}}}{\partial \hat{\mathbf{w}}}=\frac{\partial {\mathbf{y}}^{\mathrm{T}}\mathbf{y}}{\partial \hat{\mathbf{w}}}-\frac{\partial {\mathbf{y}}^{\mathrm{T}}\mathbf{X}\hat{\mathbf{w}}}{\partial \hat{\mathbf{w}}}-\frac{\partial {\hat{\mathbf{w}}}^{\mathrm{T}}{\mathbf{X}}^{\mathrm{T}}\mathbf{y}}{\partial \hat{\mathbf{w}}}+\frac{\partial {\hat{\mathbf{w}}}^{\mathrm{T}}{\mathbf{X}}^{\mathrm{T}}\mathbf{X}\hat{\mathbf{w}}}{\partial \hat{\mathbf{w}}}$$

由矩阵微分公式 $\frac{\partial {\mathbf{a}}^{\mathrm{T}}\mathbf{x}}{\partial \mathbf{x}}=\frac{\partial {\mathbf{x}}^{\mathrm{T}}\mathbf{a}}{\partial \mathbf{x}}=\mathbf{a},\frac{\partial {\mathbf{x}}^{\mathrm{T}}\mathbf{A}\mathbf{x}}{\partial \mathbf{x}}=(\mathbf{A}+{\mathbf{A}}^{\mathrm{T}})\mathbf{x}$ 可得 $\frac{\partial E_{\hat{\mathbf{w}}}}{\partial \hat{\mathbf{w}}}=0-{\mathbf{X}}^{\mathrm{T}}\mathbf{y}-{\mathbf{X}}^{\mathrm{T}}\mathbf{y}+({\mathbf{X}}^{\mathrm{T}}\mathbf{X}+{\mathbf{X}}^{\mathrm{T}}\mathbf{X})\hat{\mathbf{w}}$ $\frac{\partial E_{\hat{\mathbf{w}}}}{\partial \hat{\mathbf{w}}}=2{\mathbf{X}}^{\mathrm{T}}(\mathbf{X}\hat{\mathbf{w}}-\mathbf{y})$ 至此，求导完成，令上式等于0可得到 $\hat{w}$ 最优解的闭式解，但因为上式涉及到了 矩阵逆的计算，所以进行讨论：当 $X^{T}X$ 为 满秩矩阵或正定矩阵 时，才可以解出 ${\hat{w}}^{\ast }={\left(X^{T}X\right)}^{-1}{X}^{T}y$ ，但现实任务中往往 $X^{T}X$ 不是满秩矩阵，可以解出多个 ${\hat{w}}^{\ast }$ ，这时，选择哪一个解作为输出，将由机器学习的偏好决定，也就是引入的 正则化项。

2 广义线性模型

为了简便，我们将线性回归模型简写为： $y=w^{T}x+b$ 头脑风暴 一下，线性回归模型，其本质上我们是希望 用线性回归模型的预测值去逼近真实标记 $y$ ，那么，我们 能不能用线性模型去逼近真实标记 $y$ 的衍生物呢？可以记为： $g\left(y\right)=w^{T}x+b$ 假设 $g\left(\cdot \right)=\ln \left(\cdot \right)$ ，就相当于我们将 输出标记的对数作为线性模型逼近的目标，即 $\ln \left(y\right)=w^{T}x+b$ 这样得到的模型就是 广义线性模型，其中 $g\left(\cdot \right)$ 称为 联系函数 ，一般的，我们希望联系函数能够 单调可微，单调：是因为线性模型是单调的，经过联系函数后依然保持单调，这样去拟合才是合理的；可微：这时为了方便求导，可以使用随机梯度下降这类通过迭代的优化算法去求解。

💡其它的也是如此，我们只需要变换不同的联系函数，就使得线性函数具备了拟合 非线性 的能力

3 对数几率”回归”

🦉 有了以上的基础，我们来 审查 一下最简单的 对数几率回归 为什么是这样来做的。

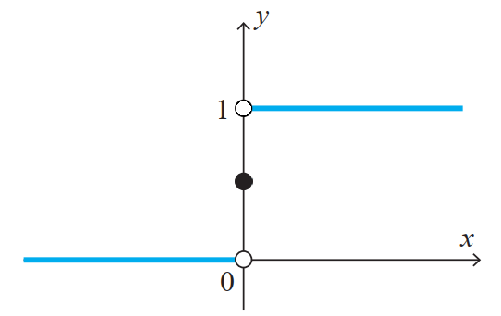
🚩 首先，该模型虽然叫回归，但实际上是解决 分类 问题的，用最简单的二分类问题来看，分为 正类和负类，那以0为界，大于0的我们认为是正类，用取值1来表示，小于0的认为是负类，取值0来表示，为了保证所有点都有定义，所以0点认为取值为0.5，这其实就是 单位阶跃函数，也是我们初步划定的 $y$ 的 真实分布，画出来如下图：

但是，我们现在要用线性模型来拟合该分布，比较困难，我们希望该分布 单调可微，所以我们寻找一个新的函数来近似该分布，就是 对数几率函数，其最大的特点就是在整个函数区间上 连续单调可微

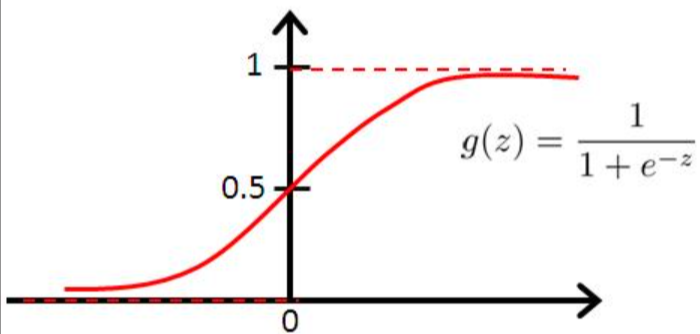
其中 $z=w^{T}x+b$，我们将该函数进行变换，来看一下具体的联系函数是什么：

y=\frac{1}{1+e^{-\left(w^{T} x+b\right)}} \\ \frac{1}{y}=1+e^{-\left(w^{T} x+b\right)} \\ \ln \left(\frac{1}{y}-1\right)=-\left(w^{T} x+b\right) \\ \ln \frac{y}{1-y}=w^{T} x+b \end{array}$$ 上式中，如果将 $y$ 视为样本 $x$ 作为正例的可能性，则 $1-y$ 就是其反例的可能性，两者的比值 $\frac{y}{1-y}$ 就称为 `几率`，几率再取 `对数`，因为对数计算是单调的，所以对几率的数学性质没有影响，这就是 `对数几率回归`，该联系函数就是： $g\left ( y \right ) = \ln \frac{y}{1-y}$ 。 目前，我们仅仅是写出了该模型的数学表达式，还未写出目标函数，如果按照 `最小二乘法` 进行优化求解，我们的步骤就应该是列出式子，求导，找极值点；但是，可以那么做有一个前提，列出的目标函数需要是 **凸函数**，这样才能保证其极值点是最小值点或最大值点 ![[Pasted image 20231121145522.png]] ❌❌❌ *我自己试了一下，列出目标函数后，暂时不知道如何形式化证明出该函数不是凸函数* 🚩 既然 `最小二乘估计` 不能用（其实大多数问题都不太能，属性过多后，很难求解逆矩阵，就算能求出来，计算量也很大，对于计算机，我们更偏向于使用通过迭代进行求解的办法），所以这里我们使用 **极大似然法** --- 简单理解 `极大似然法` 的核心思想： $$\max \left [ P\left ( 真的正 \right ) P\left ( 预测为正 \right ) + P\left ( 真的负 \right ) P\left ( 预测为负 \right ) \right ]$$ 上式表达的思想：*如果真的是正类，则应该尽可能预测为正类；如果真的是负类，则应该尽可能预测为负类*，我们使这式子最大化。（一般情况下，我们会取对数，因为概率可能是很小的值，两个很小的值相乘，在计算机里可能就为0了，所以取对数，变为两个概率相加，可以解决这一问题，同时，并不影响其数学性质） --- 利用 `极大似然法` 的思想，我们来构建目标函数，上式已经写道： $\ln \frac{y}{1-y}=w^{T} x+b$ ，其中将 $y$ 视为正类的后验概率估计，$1-y$ 代表了负类的后验概率估计，则可以重写为： $$\begin{aligned} \ln \frac{p\left ( y=1\mid x \right)}{p\left ( y=0\mid x \right)} = w^{T}+b \\ p\left ( y=1\mid x \right) = \frac{e^{w^{T}+b}}{1+e^{w^{T}+b}} \\ p\left ( y=0\mid x \right) = \frac{1}{1+e^{w^{T}+b}} \end{aligned}$$ 模型的预测概率已经表示出来了，我们最大化 `对数似然`，写出目标函数如下： $$\ell(\boldsymbol{\beta})=\sum_{i=1}^{m}\ln\left(y_ip_1(\hat{\boldsymbol x}_i;\boldsymbol{\beta})+(1-y_i)p_0(\hat{\boldsymbol x}_i;\boldsymbol{\beta})\right)$$ 其中 $p_1(\hat{\boldsymbol x}_i;\boldsymbol{\beta})=\cfrac{e^{\boldsymbol{\beta}^{\mathrm{T}}\hat{\boldsymbol x}_i}}{1+e^{\boldsymbol{\beta}^{\mathrm{T}}\hat{\boldsymbol x}_i}},p_0(\hat{\boldsymbol x}_i;\boldsymbol{\beta})=\cfrac{1}{1+e^{\boldsymbol{\beta}^{\mathrm{T}}\hat{\boldsymbol x}_i}}$ ，代入上式可得： $$\begin{aligned} \ell(\boldsymbol{\beta})&=\sum_{i=1}^{m}\ln\left(\cfrac{y_ie^{\boldsymbol{\beta}^{\mathrm{T}}\hat{\boldsymbol x}_i}+1-y_i}{1+e^{\boldsymbol{\beta}^{\mathrm{T}}\hat{\boldsymbol x}_i}}\right) \\ &=\sum_{i=1}^{m}\left(\ln(y_ie^{\boldsymbol{\beta}^{\mathrm{T}}\hat{\boldsymbol x}_i}+1-y_i)-\ln(1+e^{\boldsymbol{\beta}^{\mathrm{T}}\hat{\boldsymbol x}_i})\right) \end{aligned}$$ 由于 $y_i=0或1$ ，则： $$ \ell(\boldsymbol{\beta}) = \begin{cases} \sum_{i=1}^{m}(-\ln(1+e^{\boldsymbol{\beta}^{\mathrm{T}}\hat{\boldsymbol x}_i})), & y_i=0 \\ \sum_{i=1}^{m}(\boldsymbol{\beta}^{\mathrm{T}}\hat{\boldsymbol x}_i-\ln(1+e^{\boldsymbol{\beta}^{\mathrm{T}}\hat{\boldsymbol x}_i})), & y_i=1 \end{cases} $$ 两式综合可得 $$ \ell(\boldsymbol{\beta})=\sum_{i=1}^{m}\left(y_i\boldsymbol{\beta}^{\mathrm{T}}\hat{\boldsymbol x}_i-\ln(1+e^{\boldsymbol{\beta}^{\mathrm{T}}\hat{\boldsymbol x}_i})\right) $$ 通常情况下，我们都是对目标函数（损失函数）求最小值，所以在上式中添加负号即可： $$\begin{aligned} \ell(\boldsymbol{\beta})&=\sum_{i=1}^{m}\left(\ln(1+e^{\boldsymbol{\beta}^{\mathrm{T}}\hat{\boldsymbol x}_i})-y_i\boldsymbol{\beta}^{\mathrm{T}}\hat{\boldsymbol x}_i\right) \\ &=\sum_{i=1}^{m}\left(\ln(1+e^{\boldsymbol{\beta}^{\mathrm{T}}\hat{\boldsymbol x}_i})-\ln e^{y_i\boldsymbol{\beta}^{\mathrm{T}}\hat{\boldsymbol x}_i} \right) \\ &=\sum_{i=1}^{m}\left(\ln \frac{1+e^{\boldsymbol{\beta}^{\mathrm{T}}\hat{\boldsymbol x}_i}}{e^{y_i\boldsymbol{\beta}^{\mathrm{T}}\hat{\boldsymbol x}_i}} \right) \\ &=\sum_{i=1}^{m}\left(\ln \frac{1+e^{f\left ( x_i \right )}}{e^{y_i f\left ( x_i \right )}} \right) \end{aligned}$$ 🤓 至此，我们的目标函数已经写出来了，该函数性质特别好，它是 **高阶连续可导**，满足该条件，许多求解方法我们都可以使用了（梯度下降、牛顿法）。