0 评估方法

我们做出一个模型，如何对该模型的性能进行评估？用测试集、验证集？那这个集合应该如何划分，不同的划分方法存在什么样的问题？

0.0 留出法

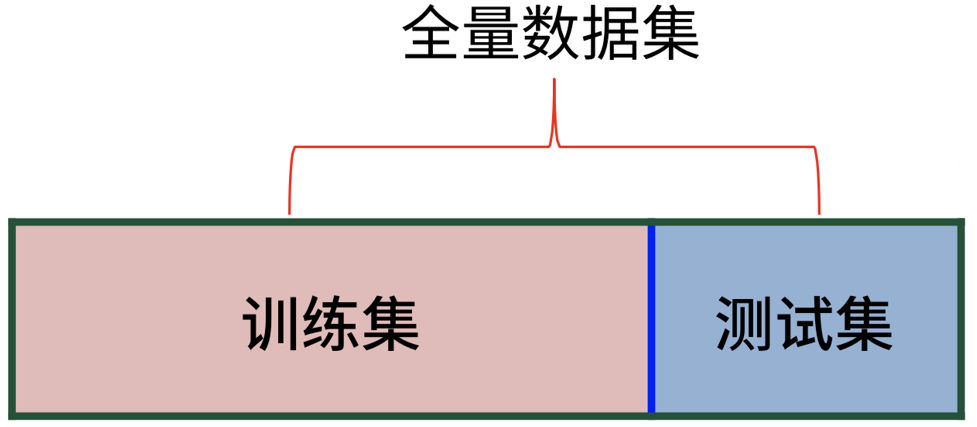
留出法：将数据集划分为两个互斥的集合，一个训练集，一个测试集，用测试集来评估测试误差，作为泛化误差的估计。

[?] 如何保证两个互斥集合数据分布的一致性？
- [n] 数据集的划分过程需要保证类别比例相似，保留类别比例的划分方式叫 分层采样
[?] 随机划分，每次划分的结果都不一样，如何降低随机所带来的偏差影响？
- [n] 重复多次实验。例如进行100次随机划分，就会产生100个模型评估结果，取这100次结果的平均
[?] 就算重复多次实验，随机划分仍然会导致部分样本重来没有出现在测试集里过？
- [i] K-折交叉验证就可以解决这个问题

0.1 K-折交叉验证

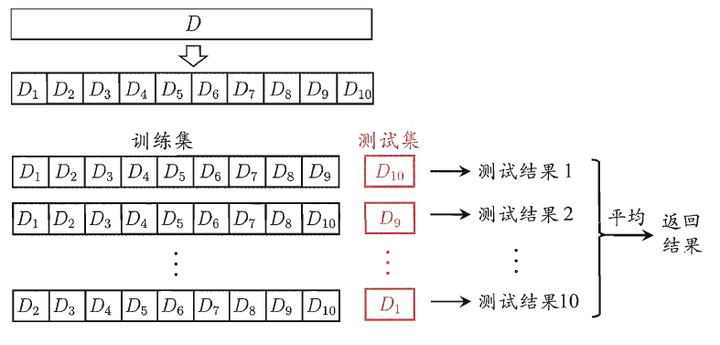
K-折交叉验证：先将数据集划分为K个互斥子集，每个子集需要保持数据分布的一致性，每次选一个集合作为测试集，最后将K次结果取平均作为模型最后的评估结果。

[?] 互斥子集的划分有多种方式，如何减小因划分方式不同而引入的偏差？
- [n] 留出法用多次实验取平均来淡化偏差，这里也一样，采用多次实验。如随机划分10次，每次做10折交叉验证，这就是10次10折交叉验证
[?] K值应该如何取值？
- [n] 如果K取值特别大，最大情况下，每个集合里只有一个样本，每次只有一个样本作为测试集，这叫“留一法”，优点是绝大部分数据都用来训练了，训练出的模型应当是最接近真实的，缺点是计算量很大，且模型泛化能力可能比较差。
- [n] 如果K值取值特别小，最小分2折，这时和留出法就相差不大了，且可能存在训练集数据量过小的问题。
- [n] K的取值需要根据具体问题具体分析（NFL定理：没有免费的午餐：脱离具体情况，去谈论什么东西的好坏没有意义）
[“] 留出法 和 K-折交叉验证 都是留出了一定数量的样本来作为测试集，并没有将所有数据都用于训练。我们认为训练数据越接近于100%，则学习出的模型偏差越小。所以能不能就用100%的数据去训练模型，同时还能留有数据来进行测试？
- [>] 自助法可以解决该问题

0.2 自助法

自助法 ：有放回的重复抽样。我们原始数据集D中有m个元素，我们每次从D中随机抽取一个元素放入到集合D1中，这个过程是有放回的，重复m次，D1中就有了m个元素，我们将该集合作为训练集，在数量上就达到了用100%的数据去训练。但D中总有没有在D1中出现过的元素，这些元素就作为测试集。这样的估计结果称为“包外估计”。

[?] 该方法训练集和测试集的数据分布是否一致？
- [n] 不一致，自助法产生的数据改变了初始数据集的分布，会引入估计偏差
[?] 该方法什么时候适用？
- [n] 在数据集较少、难以有效划分时，可以考虑使用该方法；且该方法对集成学习有较大好处

1 性能度量

确定用什么方法来评估模型后，还需要具体的指标来衡量模型泛化能力，评判模型的“好坏”。简单的 回归任务 最常用的就是 均方误差，分类问题则常用错误率和精度来衡量。除此之外，不同任务中还有更为复杂的评估需求。

1.0 查准率/查全率/F1

[n] 查准率：预测为该类的样本中有多少确实属于该类

Precision = \frac{真正例（ TP ）}{真正例（ TP ） + 假正例（ FP ）}

[n] 查全率（召回率）：该类样本有多少被正确的预测出来

Recall = \frac{真正例（ TP ）}{真正例（ TP ） + 假反例（ FN ）}

[n] 查准率和查全率是一对矛盾的度量，为了综合考虑这两个指标，可以使用 F1度量 ，它是查准率和查全率的调和平均， $F_{β}$ 则是加权调和平均

\frac{1}{F 1} = \frac{1}{2} \cdot (\frac{1}{P} + \frac{1}{R})

\frac{1}{F _{β}} = \frac{1}{1 + β ^{2}} \cdot (\frac{1}{P} + \frac{β ^{2}}{R})

上式中， $β$ 度量了查全率对于查准率的相对重要性，当 $β = 1$ 时退化为 $F 1$ ，当 $β > 1$ 时 查全率 有更大影响，当 $β < 1$ 时 查准率 有更大影响。

📌 很多时候，我们会做多次实验，这时就得到了多个混淆矩阵，当希望评估算法的全局性能，一个简单的办法，先在各个混淆矩阵上计算各个指标，然后再做平均，这样得到的结果叫 宏查准率、宏查全率、宏F1；另一个办法是，先将各个混淆矩阵对应的元素进行平均，再基于这些平均值来计算各个指标，这样得到的结果叫 微查准率、微查全率、微F1

1.1 ROC/AUC

名词	英文	翻译
ROC	Receiver Operating Characteristic	受试者工作特征
AUC	Area Under ROC Curve	ROC曲线下面积

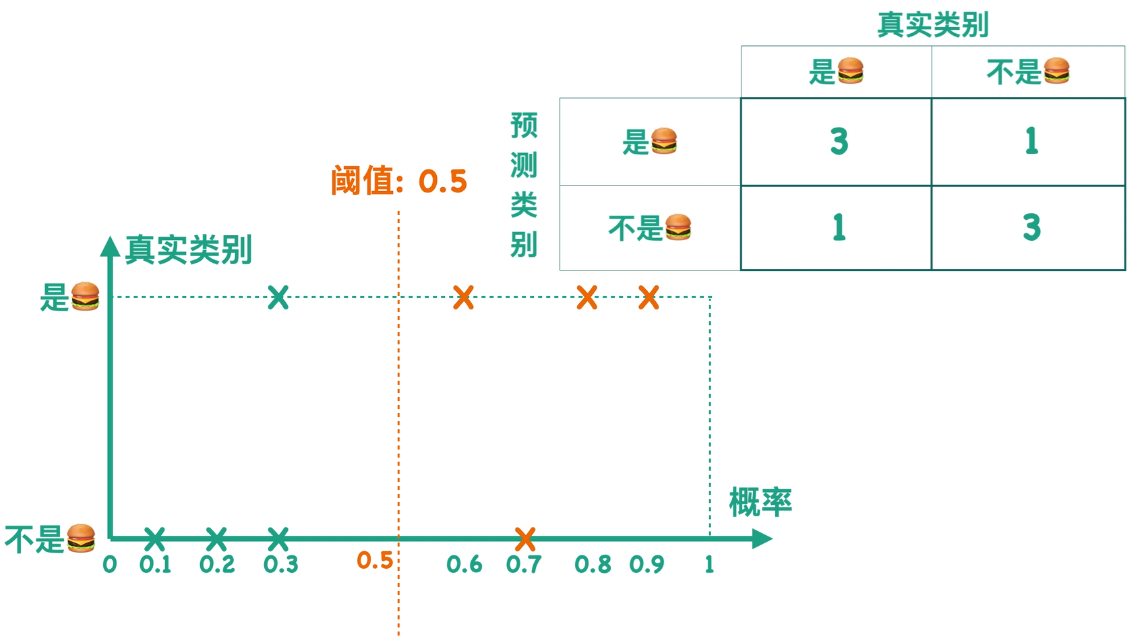
🎞️ 从上图中可以看到，在一般的 二分类 问题中，模型会给出一个样例是“正类”的概率，当概率大于一个我们设定的“阈值”时，我们就认为该样本是正例。默认情况下，该阈值为 0.5 。设定一个阈值，就对应了一个混淆矩阵，当我们的阈值从0不断变化到1时，我们就得到了多个混淆矩阵。

[*] 这里先补充两个概念，真正例率（True Positive Rate, TPR） 和 假正例率（False Positive Rate, FPR）

TPR = \frac{TP}{TP + FN} FPR = \frac{FP}{TN + FP}

当阈值为0时，全部预测为正类，这时TPR和FPR的值都为0，当阈值为1时，全部预测为负类，这时TPR和FPR的值都为1。阈值在0~1区间内连续不断的变化，我们将TPR作为纵轴，FPR作为横轴，将所有的点连接起来，就得到了ROC曲线

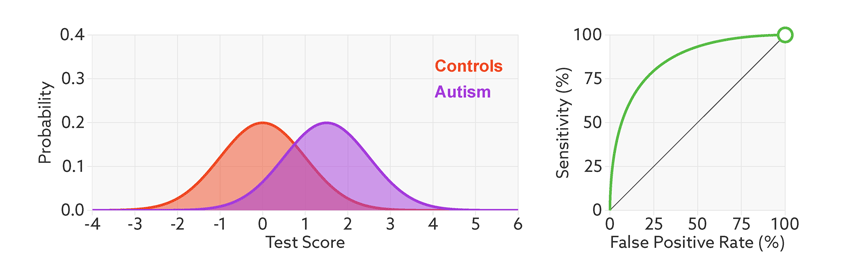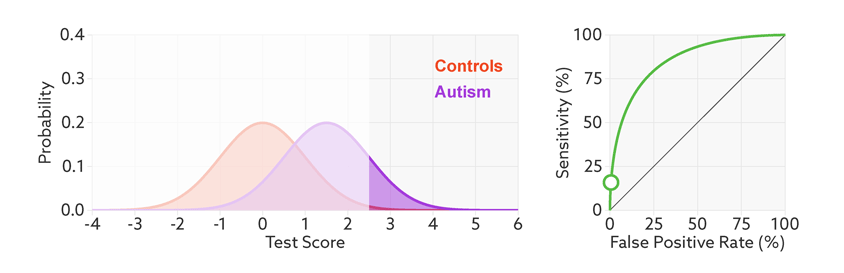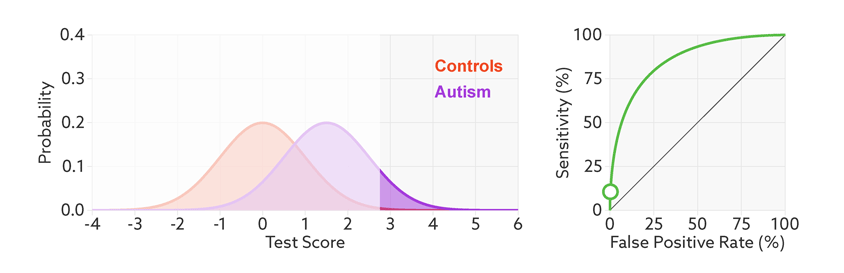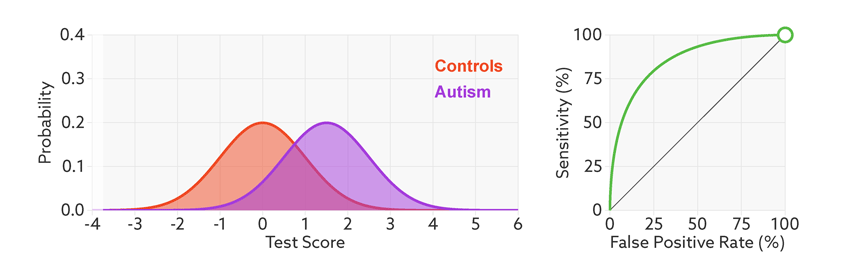
📌📌📌 不同模型绘制出的 ROC 曲线自然不同，为了通过该曲线来判别模型的“好坏”，我们需要分析 TPR和FPR 的计算公式，我们希望 TP 越来越大，FP 越来越小，其中分母是定值，所以希望 TPR 越大且 FPR 越小，反应到图形上就是 ROC曲线越靠近左上角越好，为了便于量化，我们将曲线下方的面积记为 AUC，即 AUC 值越大，模型相对来说就越好

2 比较检验

[?] 在某种度量下取得评估结果后，是否可以直接比较以评判不同算法的优劣？
- [>] 答案：不可以
- [n] 测试性能不等于泛化性能
- [n] 测试性能会随着测试集的改变而改变
- [*] 解决办法：使用 统计假设检验（hypothesis test） 。假设检验是一种统计推断方法，主要用于判断样本与样本、样本与总体的差异是由抽样误差引起还是本质差别造成的

pass，后面再补充

🚀 KK ~

探索

00-🎢模型评估